Neuron

An artificial neuron is a mathematical function that mimics the behavior of a biological neuron in our brain.
It receives multiple inputs, processes them using weights, adds bias, and passes them through an activation function to produce an output.

It is the core building block of any neural network.

Image Credit

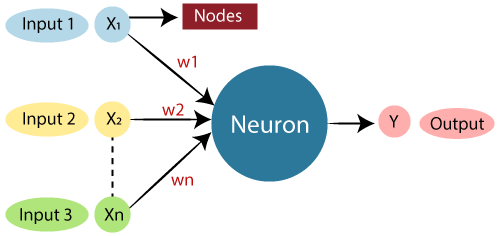
Structure of an Artificial Neuron

Inputs:
- Data (features), e.g., Age, Income, etc.
Weights:
- Importance given to each input.
Summation:
- Weighted sum of inputs:

\[\large z = \underset{i=1}{\sum}^{n} w{\scriptstyle i} x{\scriptstyle i} + b\]

Where:

w_i = weight
x_i = input
b = bias

Activation Function:
- Applies a function to add non-linearity (like decision-making).
- Examples: Sigmoid, ReLU, Tanh.
Output:
- Result after applying activation function.

Mathematical Formula

\[\large \text{Output} = \text{Activation} \left(\underset{i=1}{\sum}^{n} w{\scriptstyle i} x{\scriptstyle i} + b\right)\]

Where:

w_i = weight
x_i = input
b = bias
Activation() = function like Sigmoid, ReLU

Analogy:

Imagine you are a teacher grading students based on: - Homework (weight = 0.4) - Exam (weight = 0.6)

You add the scores with different importance:

Final Grade = (Homework × 0.4) + (Exam × 0.6)

If the result is above a threshold, you decide Pass; else, Fail.

This is what a neuron does!

Key Concepts in Artificial Neuron

Component	Role
Inputs (x1, x2, …)	Raw data
Weights (w1, w2, …)	Importance of each input
Bias (b)	Adjustment to the output
Summation	Weighted sum of inputs and bias
Activation Function	Adds non-linearity (like decision-making)
Output	Final result

Why do we use Activation Functions in Neurons?

Without activation function: The neuron would behave like a simple linear equation (a straight line).
With activation function: Neuron can model non-linear relationships.
This makes the model powerful enough to solve complex problems like image or speech recognition.

Visual Representation of an Artificial Neuron

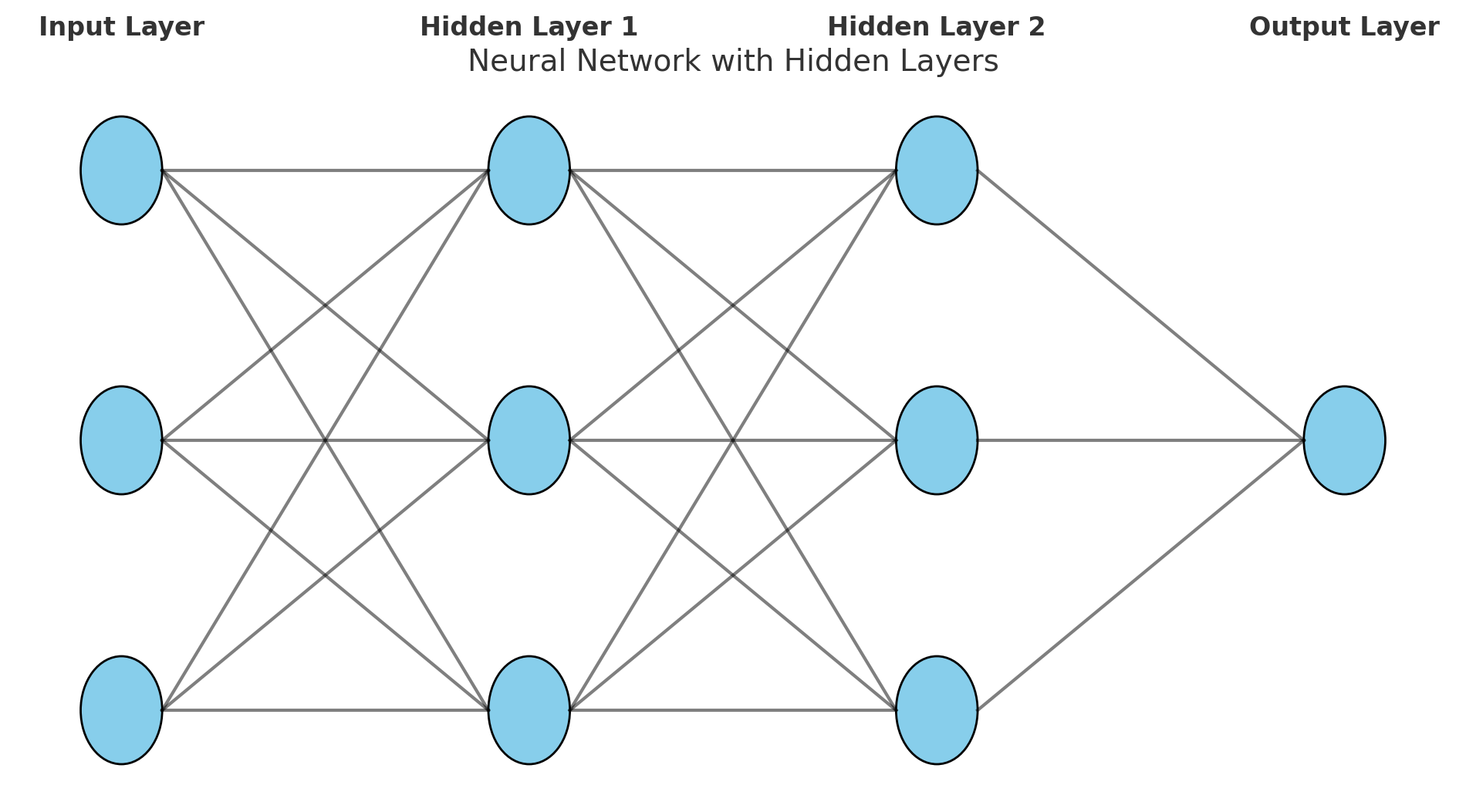
Why So Many Neurons in One Hidden Layer?

1. Each Neuron Learns a Pattern (Feature Extractor)

Every neuron in a hidden layer learns a specific pattern or relationship between input features.
Example:
- One neuron might learn how Glucose affects Diabetes.
- Another might learn how BMI interacts with Age.
- Another might learn combined effects (e.g., high insulin + high glucose).

More neurons → More patterns/features can be learned.

2. Complex Data Requires More Capacity

Real-world data (like health data) is not linearly separable.
Complex relationships need more neurons to model non-linear boundaries.
Example: A single neuron can model a line, but many neurons together can model curves, clusters, and intricate decision boundaries.

More neurons → Better ability to capture complex patterns.

3. Universal Approximation Theorem

The theorem states that a neural network with at least one hidden layer with sufficient neurons can approximate any continuous function.
But this doesn’t mean infinite neurons are good. Balance is key.

Layer	Typical Neurons Example	Why?
Input Layer	Matches number of features (e.g., 8 for diabetes dataset)	1 neuron per feature
Hidden Layer 1	2x-3x of input neurons (e.g., 16)	Capture various combinations of features
Hidden Layer 2	Smaller than first hidden layer (e.g., 8)	Condense and refine patterns
Output Layer	Depends on task (1 neuron for binary classification)	Gives the final prediction

Analogy

Imagine neurons are workers in a factory.
More workers (neurons) can process more raw materials (input features).
Too few workers → can’t handle complex tasks.
Too many workers → waste of resources, possible errors (overfitting).

Be careful

Problem	Cause	Solution
Underfitting	Too few neurons, model too simple	Add more neurons/layers
Overfitting	Too many neurons, model memorizes data	Reduce neurons, add regularization methods

More neurons in hidden layers → better at learning complex patterns.
But too many neurons → risk of overfitting.
You want just enough neurons to learn well but generalize well.

Thumb Rules for Choosing Number of Neurons in Hidden Layers

1. Rule of Pyramid Shape

First hidden layer: 2x to 3x the number of input features.
Subsequent hidden layers: Gradually decrease the number of neurons.
Forms a pyramid shape from input to output.
Example (for Diabetes Dataset with 8 features):
- Hidden Layer 1: 16-24 neurons
- Hidden Layer 2: 8-12 neurons
- Output Layer: 1 neuron (binary classification)

2. Between Input & Output Size

A simple formula to start:

\[\large \text {Neurons in Hidden Layer} = \frac{Input Neurons + Output Neurons}{2}\]

For Diabetes Dataset:
- Input = 8, Output = 1 → Hidden Layer ≈ 4-5 neurons.
Simple, fast, and works for basic problems.

3. Heuristic: Power of 2

Start with neuron counts like 8, 16, 32, 64.
Common in deep learning.
Easy to scale and optimize later.

4. Don’t Over-Engineer Early

Start small (e.g., 1 hidden layer, 8-16 neurons).
Increase only if:
- Model underfits (low train accuracy & high error).
- Model can’t learn patterns.

5. Empirical Tuning is Key

Use grid search or random search for tuning neurons.
Monitor validation accuracy & loss curves.
Avoid blindly adding neurons.

6. Regularization is Important

If using too many neurons:
- Add Dropout layers.
- Use L2 regularization (Ridge penalty).
Helps prevent overfitting.

Dataset Size	Recommended Neurons (Hidden Layer 1)	Why?
Small (<1k samples)	1-2x input features	Avoid overfitting
Medium (10k samples)	2-3x input features	Balance complexity & generalization
Large (>100k samples)	Start with higher (32-64 neurons)	Can afford more capacity without overfitting

Why Do We Need Many Hidden Layers in Neural Networks?

1. Shallow vs Deep Neural Networks

A shallow network has only 1 hidden layer.
A deep neural network has 2 or more hidden layers.
Adding depth (more layers) enables the model to learn hierarchical features.

2. Simple Problems → Few Layers

For simple linear problems (e.g., linear regression), a single hidden layer might be enough.
But real-world problems (images, speech, text, medical data) involve complex non-linear patterns.

3. Why More Hidden Layers?

Hidden Layers	Role / Purpose
1st hidden layer	Learns basic features (e.g., edges in images, basic relations in data)
2nd hidden layer	Learns more abstract features (e.g., shapes, combinations of previous features)
3rd & beyond	Learns complex patterns (e.g., object parts, interactions, high-level concepts)

Each layer builds upon previous layers.
More hidden layers → More abstract & high-level features.

4. Real-World Example

Image Recognition:
- Layer 1: Detects edges, colors.
- Layer 2: Detects shapes (circles, squares).
- Layer 3: Detects objects (eyes, mouth, wheels).
- Output: Classifies image (cat, dog, car).

5. Mathematical Justification

Universal Approximation Theorem says 1 hidden layer can approximate any function.
But deep networks are more efficient:
- They require fewer neurons per layer.
- Better at reusing features.
- More scalable for complex tasks.

6. Practical Reasons for Many Layers

Reason	Why It Helps
Hierarchical Learning	Learns from simple to complex patterns step-by-step.
Reusability of Features	Lower layers learn features reused by higher layers.
Better Representations	Can model very complex non-linear relationships.
Scalability	Easier to handle large datasets & tasks.

7. But Beware of Overfitting!

More layers → More parameters → Higher risk of overfitting.
Solution:
- Use Dropout, Batch Normalization, Regularization.
- Increase data (Data Augmentation).
More hidden layers help neural networks learn complex, abstract patterns.
Useful for tasks like image recognition, speech, language understanding, and medical predictions.

Key Takeaways:

Neuron is the smallest unit in an Artificial Neural Network.
It transforms inputs into meaningful outputs using weights, bias, and activation function.
Multiple neurons connected together form layers that can solve very complex tasks like face recognition, language translation, etc.

Deep Learning

Fundamentals of Deep Learning.